Correlation and Spatial Autocorrelation

Introduction

  There are two parts to this assignment. The first part will consist of using IBM SPSS Statistics Viewer to calculate correlation statistics and significance levels for Milwaukee census tract demographic data and then describing the results and the second part will consist of using spatial autocorrelation with Texas Election Commission (TEC) data for the 1980 and 2016 elections. The patterns found in the TEC data will also be described and analyzed. A series maps will be created to help promote discussion.

Using IBM SPSS to Explain Milwaukee Demographics

  Figure 5.1 shows the correlation matrix with all of the demographic information from the Milwaukee Excel sheet. Correlation is described based on strength and direction. The strength of a correlation is either positive, negative, or null. A positive correlation means that as one variable increases, the other does as well. A negative correlation means that as one variable increases, the other decreases. A null correlation means that there is no statistical correlation between the two variables. The significance level tells the user how significant the correlation is. If the significance value is less than .05, then the correlation r value is significant at the 95% level. This implies that the chance for a false positive is less than 1 in 20.

Fig 5.0: Demographic Correlation Chart

  This chart provides the Pearson Correlation (r values), the significance level (95% confidence level, two tailed), and the number of samples for each correlation. In the Pearson correlation, the number of stars refers to the level which the correlation value is significant to. One star means that the value is significant to the .05 level and two stars mean that the value is significant to the .01 level. The significance level also indicates the results of a hypothesis test performed by the SPSS software. If the significance value is less than or equal to .05, the null hypothesis is rejected which means that there is a statistical correlation between the two variables. If the significance value is greater than .05, then the result is that one fails to reject the null hypothesis meaning that there is no statistical correlation between the two variables.
  Based off of the chart, the number of manufacturing employees (Manu) has moderate positive correlation with the number of retail employees (Retail), a moderate positive correlation with the number of finance employees (Finance), a strong positive correlation with the White population (White), a weak negative correlation with the the Black population (Black), a weak positive correlation with the Hispanic population (Hispanic), and a weak positive correlation with median household income (Medinc).
  The number of retail employees has a moderate positive correlation with the number of finance employees, a strong positive correlation with the White population, a very weak negative correlation with the Black population, a null correlation with the Hispanic population, and a very weak positive correlation with median household income.
  The number of finance employees has a strong positive correlation with the White population, a very weak negative correlation with the Black population, a very weak negative correlation with the Hispanic population, and a moderate positive correlation with median household income.
  The White population has a moderate negative correlation with the Black population, a very weak positive to null correlation with the Hispanic population, and a moderate positive correlation with median household income. The Black population has a very weak negative correlation with the Hispanic population and has a weak correlation with median household income. Lastly, the Hispanic population has a null relationship with median household income.
  Although its nice to know the strength and direction of correlation between two variables, choosing stand out trends to analyze is more beneficial and informational. For example, the Black population has a negative correlation with everything. Also, all of the Black population correlation values are significant to the .01 level. This means that where there is a larger Black population, there is lower median household income, less retail employees, less manufacturing employees, less finance employees, and less people of White and Hispanic races. Another stand out trend is that the White population has a positive correlation with everything except the Black population. All of the White population correlation values are at least significant to the .05 level. This means that where there is a larger White population there is a larger Hispanic population, greater median household income, greater number of manufacturing employees, increased number of retail employees, and an increased number of finance employees. Looking at the Hispanic population correlations, there is a mix between positive and negative correlation across all demographic categories.

Spatial Autocorrelation

Introduction

  The  hypothetical scenario for this question is that the author has been given access to election data from the Texas Election Commission (TEC) from 1980 and 2016. The TEC want to know the trends of the percentage of the democratic vote, the overall percentage of voter turnout, and the percent Hispanic voters. The TEC want to know how these variables have changed over the past 36 years. To analyze these trends, both GeoDa and SPSS software will be used to see if there is any clustering with the variables, or any correlation between them.

Methods
  The Texas election data was given as part of this assignment. However, the percent Hispanic population by county estimates had to be downloaded from the Census Fact Finder's website. The Texas county shapefiles also had to downloaded from this site. Then, the demographic data was standardized in the Excel sheets. The Texas election data, and the Hispanic population data was then joined to the Texas shapefile. The joined output was then saved as a shapefile because the GeoDa software doesn't recognize feature classes, just shapefiles. The Excel tables were then edited to only standardized even further to display only the necessary demographic data so that it would be easy to use when creating a correlation matrix with the SPSS software.
  Next, the GeoDa software was used to create 5 maps and 5 Moran's I scatter plots. The variables used in these maps and charts include the perent of voter turnout for 1980 by county, the  percent of voter turnout for 2016 by county, the percent democrat vote for 1980 by county, the percent Democrat vote for 2016 by county, and the percent Hispanic population for 2015 by county.
  To create the maps and charts, first a new project was created using the saved shapefile which contained all of the demographic information. Then, because spatial autocorrelation requires a spatial weight, the county shared boundaries were used for this. This is done by going to Tools → Weights Manager → Create. Then, the Add ID Variable button was clicked on and the Poly_ID was used which is the shared county boundary. The Rook contiguity was used. Then, the Cluster Maps → Univariate Local Moran's I  was clicked on. Then, the demographic statistic which was going to mapped was chosen and the option to construct a scatter plot, and cluster map was chosen. This was done with all 5 demographic statistics.
  Lastly, SPSS was used to create a correlation matrix using the super standardized Excel spreadsheet.

Results / Discussion
  The way spatial autocorrelation works for this scenario is each county is either classified as high high, high low, low high, low low, or not classified. High high means that the county has a high value for the input variable and is surrounded by other counties that have high values. High low means that the county has a high value of the input variable, but is surrounded by counties with low values. Low high means that the county has low values of the input variable, but is surrounded by counties with high values. Low low means that the county has low values of the input variable and is surrounded by counties with other low values. Because the world, demographic information, and election data isn't random, there is clustering. Generally, it is more common so see more high high's and more low low's than it is to see low high's and high low's.
  Moran's I value is a value used to compare the value of a specific variable from one area (county), in this case it's the demographic or election statistic, with the value of other surrounding areas (neighboring counties). The Moran's I value ranges from -1 to 1 just like the correlation r value. However, they carry different meanings, The closer the Moran's I is to -1, the less clustered the data is. The closer the Moran's I is to 1, the more clustered the data is. The Moran's I doesn't indicate the direction of anything, it just indicates how clustered things are within a specified study area.
  This first map and Moran's I chart was created using Geoda to show the percent Democrate vote for 1980. The map is shown in figure 5.1, and the chart is shown in figure 5.2.

Fig 5.1: Percent Democrate Vote 1980 Spatial Autocorrelation Map

  This map shows that there is clustering of both high high's and low low's. The high high's are located mostly in the southern and eastern portion of the state. The low low's are mostly located in the northwestern part of the state and to the northwest of San Antonio. There are only two high low's and two low high's. The high high's indicate that there is a clustering of greater percent Democrat votes and the low low's indicate that there is a clustering of lesser Democrat votes.

Fig 5.2: Moran's I Chart for Percent Democrat Vote 1980

   The Moran's I chart shown above in figure 5.2 indicates that overall, the voting trend are clustered by county. A value of .575 means that there is a moderate clustering rate. It is important to remember that this Moran's I value doesn't specify the direction of the voting turnout (less or more), but it just gives the overall clustering of the data.

  This second map and chart are based on the percent Democrat vote in the 2016 election. The map is displayed in figure 5.3 and the Moran's I chart is displayed in figure 5.4.

Fig 5.3: Percent Democrat Vote 2016 Spatial Autocorrelation Map

  To no surprise, the results shown in this map are similar to that shown in the 1980 map. However, there are a few differences. First, the area of lower percent democratic vote located in the north west part of the state in 1980 have moved about 100 to 200 miles to the east. The areas of greater voter turnout have become more concentrated along the Texas - Mexico border.

 The Moran's I chart below indicates that there is a stronger moderate clustering rate between counties of higher turnout and counties of lower turnout.

Fig 5.4:  Moran's I Chart for Percent Democrat Vote 2016

  This next map shown in figure 5.5 displays the the spatial autocorrelation of percent of voter turnout by county for 1980. Clustering in this map isn't as strong as in the percent Democrat vote maps. There are two main areas of both higher voter turnout and lower voter turnout. One of the areas of higher voter turnout is located in the extreme northern portion of the state and the other is located just north of San Antonio. The first area of lower voter turnout is located in the southern region of Texas and the second area is located in the very eastern part of the state.

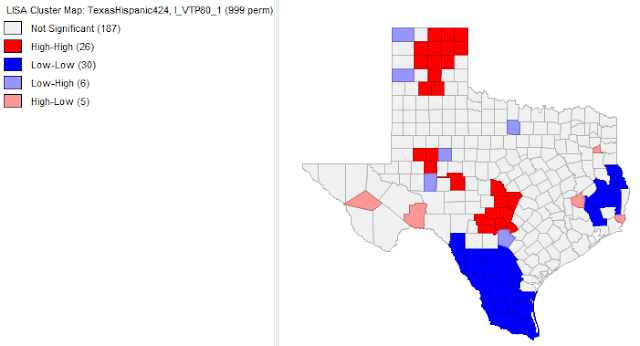Fig 5.5: Voter Turnout 1980 Spatial Autocorrelation Map

The Moran's I chart shown in figure 5.6, indicates that the clustering is weaker than the percent Democrat votes, but that clustering is still present.

Fig 5.6: Voter Turnout 1980 Moran's I Chart

  This next map, shown below in figure 5.7 shows the percent voter turnout for 2016. The trend between the 1980 map to the 2016 map is that there is less clustering in 2016. This means that the voter turnout seems to be less influenced by location in 2016 than it did in 1980. the clustering is still similar to the 1980 map, but the clustering is less defined and a little more fragmented. It is interesting to note that the difference between the counties classified as high high and low low increased by 8 counties. This means that the clustering of lower voting turnout counties has increased relative to the number of higher voting turnout counties.

Fig 5.7: Voter Turnout 2016 Spatial Autocorrelation Map

  Figure 5.8 shows the Moran's I chart. The Moran's I value decreased dramatically from .468 in 1980 to .287 in 2016. This means that there is less clustering of both higher and lower percent voter turnout in 2016 than there was in 1980. The Moran's I value of .287 indicates that there is a weak to very weak clustering rate among the percent of 2016 voter turnout in Texas counties.

Fig 5.8: Moran's I Voter Turnout 2016

  This next map, featured in figure 5.9, shows the spatial autocorrelatoin of the percent Hispanic population by county from 2015. The Hispanic percentage population by county is very clustered. The counties of higher percent Hispanic population are located almost exclusively along the Texas - Mexico border, and the counties which have a lesser percentage of Hispanic population are located in the eastern and north eastern portion of the state.

Fig 5.9: Percentage of Hispanic Population by County Cluster Map 2015

  The Moran's I chart for the percentage Hispanic population by county in 2015 is displayed below in figure 5.10. The Moran's I value of .779 indicates that there is a strong clustering rate among the percentage of Hispanics by county. This is very evident in the map in figure 5.9.

Fig 5.10:  Moran's I Percentage of Hispanic Population 2015

  Next, the super standardized Excel table was used to create a correlation matrix in SPSS to see how the five variables relate with each other. This matrix is shown below in figure 5.11. This was created so comparisons between the percent Hispanic population statistics and the map can be more easily.

Fig 5.11: Texas Election Data and Hispanic Percent Population Correlation Matrix

 The percent Hispanic has no correlation with the democratic vote in 1980. The reasons for this is because the percent Hispanic population estimates are of 2015 and the percent democratic vote of the 1980 election is from 1980. These two variables should logically have no correlation with each other which is the case.
  The percent Hispanic population has a strong positive correlation which is significant to the .01 level with the percent democratic vote for 2016. This means that there is strong overlap between the percent of the Hispanic population by county and the percent of the democratic vote. This indicates that Hispanics generally vote democrat because the relationship is strong and positive. It also would theoretically mean that the greater the percent of Hispanics there are in a county, the more likely that the county will have a larger percent democratic vote. This overlap and correlation can be seen by looking at and seeing the similarities between the two maps (Figure 5.9, and Figure 5.3). The positive overlap occurs mostly in the southern portion of the state along the Mexico - Texas border while the negative overlap occurs in the north and eastern portion of the state.
  The percent Hispanic population has a weak negative correlation with the voter turnout of 1980. This relationship doesn't mean anything and is merely a coincidence as the percent Hispanic population data is from 2015 and the voter turnout from 1980 is from 1980.
  There is a moderate negative correlation significant to the .01 level with the voter turnout of 2016. This implies that the counties which have a high percentage of Hispanics, they are more likely to have a lower percentage voter turnout. This analysis suggests that Hispanics generally have lower voter turnout.

Conclusion

  In conclusion, there are several trends identified in this lab which the TEC or governor could use to help with campaigning and identifying areas to focus on. If the governor is a democrat he or she should attempt to organize a large get out the vote event focusing in on the Hispanic population. The governor should do this because the results of this lab showed that Hispanics tend to vote democrat, but also tend to have a lower voter turnout.
  The results of this lab could also be used to see how the demographics of Texas and how it relates to election results is changing. Currently, Texas is a very republican state. For a potential future analysis, given that Hispanic population is increasing in Texas, if the rate could be found at which the Hispanic population is increasing, it would be possible to find the election year that the state of Texas would switch from being a republican state to a democratic state. This could be very useful information for the TEC, governor, and anyone that has an interest in politics.