Introduction
There are two main goals in this lab. One is to demonstrate an understanding of z-scores, and the other is to use the probability of an event occurring to determine a specific range of outcomes. The scenario in this lab consists of being hired by an independent research consortium to study the the geography of foreclosures in Dane County, Wisconsin. The Dane County government is concerned about the increase in the number of foreclosures in 2012 compared to 2011. Using the number of foreclosures by census tracts for both 2011 and 2012, the first task as a new employee is to analyze the spatial patterns of foreclosures between 2011 and 2012 and then create a prediction for the number of foreclosures in Dane County by census tract for 2013. This will be done by answering the following questions: What number of foreclosures will be exceeded 70% of the time in 2013? and What number of foreclosures will be exceeded only 20% of the time in 2013? Doing this will help to create a picture of what is happening spatially regarding foreclosures in Dane County.The end product will be a map of Dane County census tracts populated with the expected number of foreclosures and the range of percentiles associated with it for 2013. The expected 2013 values will be based on the patterns seen between 2011 and 2012. Also, a map showing the difference in the number of foreclosures by census tract between 2011 and 2012 will be created. The patterns found in these maps will then be analyzed and discussed.
To demonstrate an understanding of z-scores. The term z-score will be defined, and two z-scores a piece will be calculated for census tracts 31, 114.01, and 122.01 using the 2011 and 2012 foreclosure data. These census tracts will also be used when discussing the data in the maps.
Methods
 |
| Fig 3.0: Z-Score Equation |
Defining and Calculating Z-Scores
A z-score can be defined as a the number of standard deviations a specific observation is away from the mean. It can also be described as relative value in comparison to mean of a data set. A z-score is equal to a specific observation minus the mean of the data set all divided by the standard deviation of the data set. This equation is shown in figure 3.0 on the right. In the figure, Z represents the z-score, X represents the specific observation, µ represents the mean, and σ represents the standard deviation. A z-score is a very powerful statistic. It can be used to find the probability of a specific event occurring if the data distribution is relatively normal. Z-scores are not assigned a unit. Rather, it is a relative number to the mean. In this lab, one of the goals is to calculate the z-scores of the specific census tracts 31, 114,01, and 122.01 for both 2011 and 2012 foreclosures. This calculation is shown below in figure 3.1 for all six z-scores. The mean and standard deviation were calculated in Excel after exporting the attribute table for the Dane County shapefile. These values were then doubled checked in ArcMap under the symbology tab. The unit for the mean, standard deviation, and observations is the number of foreclosures.
 |
| Fig 3.1: Z-Score Calculations |
Calculating the Difference in Foreclosures Between 2011 and 2012, and Predicting 2013
To help with analysis of the foreclosures, a new field was created in ArcMap which contained the difference between the foreclosures from 2011 to 2012. This was done by taking the Count2012 and then subtracting the Count2011 field from it. This new field makes it easy to identify which tracts had an increase in foreclosures and which tracts had a decrease in foreclosures.
This difference field was then used to predict the number of foreclosures by tract for 2013. Assuming the patterns from 2011 to 2012 stay the same from 2012 to 2013, the 2013 predicted value can be calculated by extrapolating the trend from 2011 to 2012. This consists of adding the Count2012 value with the difference value to get the predicted 2013 value. These predicted values will be used when calculating the percentile probabilities and when creating the prediction map with the percentiles and predicted values.
Determining a Range of Outcomes Based on a Probability Using Z-Scores
As noted before, z-scores can be a powerful statistic. This is because they can be used to help determine a range of outcomes given a probability. For this lab, z-scores will be used to determine which census tracts will fall within the top 70%, and top 20% when looking at the number of foreclosures by census tract in Dane county, Wisconsin.
This is done by using the z-score equation in figure 3.0. However, instead of solving for the z-score "Z", the equation will be solved for a specific observation "X" which will be the break value when determining the percentile range. Another twist in the equation is that only the mean and standard deviation are given or have already been calculated based on the data. Luckily there is a way to look up a z-score based on the given probability. This can be done using a z-score chart shown below in figure 3.2. The probability of a exceeding a specific observation is shown in the chart with the numbers that have four decimal places. The z-score can be found by finding the probability in the chart and then looking to the corresponding value at the top row and at the far left column.
For example, wanting to find the z-score for a value in which the probability of exceeding is 51%, one would first look for .51 on the table. Often, the exact probability isn't given in the chart, so using the value just below is generally acceptable. In this case the closest number to .51 without going over is .5080 found in the third column in the first row. Looking at the corresponding value in the top row and the far left column, the z-score of 0.02 can be identified. However, this is not the right z-score. Because the value being sought after is on the left side of the mean, that means that this z-score has to be multiplied by -1 to find the correct z-score. This quirk has to only be done when the value being looked for is less than the mean. This can be identified by looking at the probability. If the probability is 51% or greater, then the sought after observation will fall to the left of the mean.
If the probability wanted is 49% or less then the compliment of the probability can be used to find the z-score. For example, to find a z-score for a value in which the probability of exceeding is 10%, one would take 1 - .1 to calculate .9. The number .9 would then be used in the chart. The closest probability to .9 without going over is .8997 which is found on the right side of the chart. Looking at the corresponding value at the top row and the far left column, a z-score of 1.28 can be determined. This is the z-score for the value which the top 10% of all values in the original data set are greater than or equal to.
 |
| Fig 3.2: Z-Score Lookup Table |
Now, all the values needed to solve for the breaking point value using the z-score equation are given. Because these probabilities will be based off of the 2013 prediction, the 2013 predicted values will be used to determine the mean and standard deviation. Using the statistics feature in ArcMap, the mean is 13.206 and the standard deviation is 13.409. The calculation for solving for the breaking point observations can be seen below in figure 3.3. Once again, the units for X, µ, and σ is the number of foreclosures. With these X values solved for, it can now be said that the top 70% of the number of foreclosures by census tract in Dane county will be at least 7. Because there cannot be .23 foreclosures the number is rounded up. If it's rounded down the value wouldn't be in the top 70%. It can also be said that the top 20% of the number of foreclosures by census tract in Dane county will be at least 25.
 |
| Fig 3.3: Calculating Breaking Point Values |
Results/Discussion
Tying the z-scores calculated from the three census tracts shown in figure 3.0 back to study question, it is clear that these census tracts have great variation when comparing them with each other and to the rest of the tracts. Tract 31 had 24 foreclosures in 2011 and 18 foreclosures in 2012. Both years, these values fell above the average. The z-score changed dramatically from 1.437 in 2011 to 0.575 in 2012. Tract 144.01 had 32 foreclosures in 2011 and 39 foreclosures in 2012. These values were well above the mean for both years. The z-score slightly increased from 2011 to 2012. Lastly, tract 122.01 had 6 foreclosures for both 2011 and 2012. The z-score slid ever so slightly from 2011 to 2012. Because the number of foreclosures stayed the same for tract 122.01 but the z-score went down, one can conclude that the overall number of foreclosures increased from 2011 to 2012. This is also evidenced by the change in the mean from 11.393 to 12.299. These random census tracts are also evidence that not every census tract is experiencing an increase in foreclosures.Using the values calculated in the difference field, a diverging color scheme map was created to show the difference in the number of foreclosures from 2011 to 2012. The green to red color scheme was chosen because generally, green is associated with good things and red is associated with bad things. The green hues show census tracts which had a decrease in the number of foreclosures and the red hues show the census tracts which experienced an increase in the number of foreclosures. The yellow hue shows which tracts experienced very little difference in the number of foreclosures. Looking at the three tracts: 31, 114.01, and 122.01, they are all placed within three different classifications. Tract 31 is in an interesting location. Though tract 31 decreased in the number of foreclosures, every census tract immediately surrounding it either had the same number of foreclosures or had an increased number of foreclosures.
Without having any other data to compare the foreclosure numbers to, the reason for the increase in foreclosures cannot be determined. Also, this map doesn't show how many foreclosures there were in each census tract, it only shows the difference. Hence, a tract which had 100 foreclosures could be in the same category as a tract than had only 3 foreclosures. However, this map does a good job at showing that there is a large increase in the number of foreclosures. There are a total of 8 tracts which had an increase of foreclosures between 10 to 16 compared to only 3 tracts which had a decrease in foreclosures between 9 and 14. The change in these extreme tiers is a strong sign that the number of foreclosures is rising between 2011 and 2012.
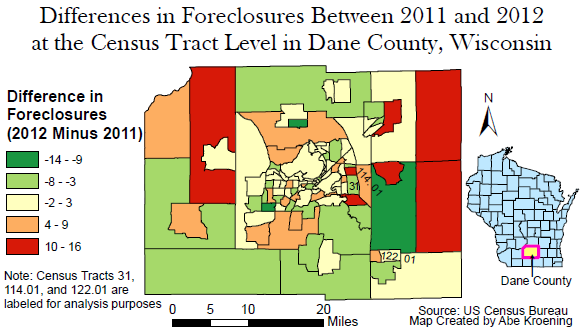 |
| Fig 3.4: Differences in Foreclosures Map |
 |
| Fig 3.5: Predicted 2013 Percentiles and Number of Foreclosures |
Conclusion
In conclusion, unfortunately for the Dane county officials, the number of foreclosures is predicted to be on the rise in 2013. There were 97 more foreclosures in 2012 than there were in 2011. Based off this data, the pattern was extrapolated to create a prediction for 2013. This prediction calls for the census tracts which experienced an increase in the number of foreclosures to continue increasing at the same rate, and for the census tracts which experienced a decrease in the number of foreclosures to continue decreasing at the same rate.
Based off of these findings, if the 2011 to 2012 patterns continue, this could be very bad news for Dane county. Likely, many people will be left looking for new homes, and will be forced to move out of the county in order to find cheaper housing. This could impact the local economy and job market in a negative manner.
Also, it is most likely be advantageous to the county to reverse this trend by encouraging people to continue to live in Dane county. They could lower their county taxes, or try to create higher paying jobs within the county. This could be done through government legislation or by advocating larger companies to move to the county.
Sources
Think Calculator, Z-Score Formula
US Census Bureau
No comments:
Post a Comment